The Adaptive Radix Tree: ARTful Indexing for Main-Memory Databases
摘要: 主存容量已经涨到了一个能把大部分数据库放到RAM中的时代。对于内存数据库系统来说,索引的性能是一个关键的瓶颈点。传统的内存索引结构比如平衡二叉树在现代硬件上效率比较低,因为他们并没有利用好CPU的cache。哈希表,也经常用于主存索引,足够快,但只能提供点查询。
为了克服上面的缺点,我们在这里介绍一下ART,Adaptive Radix Tree (trie) 可以有效的作为主存的查询索引。他的查找性能被高度优化,只读搜索树,支持高效的插入和删除。同时ART通过动态的压缩内部节点使得他的空间使用率很高,解决了Radix Tree通常对于空间占用很高的问题。不但ART的性能可以和哈希表相媲美,他还把数据保存成了排序的格式,这可以让范围查询和前缀搜索更有效率。
1. 介绍
经过几十年主存容量的增加,即使是大型的事务数据库也能把索引放到RAM中。当大部分数据都被Cache了以后,传统的数据库系统就变成了CPU密集型的应用,因为他们他们花费了很多的努力来避免磁盘IO。这也引领了在主存数据库方面非常激烈的研究和商业行为,像H-Store/VoltDB,SAP HANA和HyPer。这些系统基于新硬件趋势和更快来优化。比如我们的系统HyPer,把事务编译成了机器码避免了Buffer管理,锁和同步机制消耗过多等问题。针对于OLTP的工作负载,生成的查询计划一般是顺序的索引操作。所以,索引的效率是性能的重要因素。
25年前,T-Tree作为一个内存索引结构被提出来。不幸的是,戏剧性的处理器架构重新渲染了 T-Tree,像其他的二叉树一样,在现代硬件上效率很低。原因是一直增长的CPU cache和主存的访问速度分道扬镳,通用的内存访问速度的假设也就过时了。B+Tree的变体比如cache敏感的B+Tree对于内存的cache更加友好,但是需要跟昂贵的更新代价。更严重的是,不管是二叉树还是B+Tree都被另一个CPU特性拖累:因为比较的结果不能被精准的预测,所以现代的CPU的流水线就很容易停顿,这会引起额外的延迟。
这些传统查找树的问题被最近的一些基于现代硬件架构的数据结构解决掉了。K路的查找树和Fast Architecture Sensitive Tree (FAST)用数据的层级并行(SIMD)实现了同时做多个比较。而且FAST用了一个利用cacheline和TLB优化的数据结构来避免cache miss。尽管这些优化的索引结构可以提高查询的效率,但不能支持增量更新。对于一个OLTP的数据库系统来说,持续的插入,更新和删除都是必要的,一个明显的方法就是类似差速器文件的机制,但这会引起额外的损失。
哈希表是另一个流行的主存索引结构。和查找树O(logn)的查找时间相比,哈希表只有O(1)的查找时间,所以在主存中更快。尽管如此,哈希表在数据库索引中用的并不多。一个原因是哈希表把key随机的散列开了,所以就只能支持点查询。另一个原因是哈希表不能很好的处理扩容,不需要需要额外的重新组织的内存和O(n)的复杂度。因此现在的系统面临一个不幸的取舍,在哈希表的快速点查询和相对来说慢一点的功能齐全的查找树之间。
第三种数据结构的类型,被称为trie,radix tree,prefix tree,digital search tree,在表1中。

这些数据结构直接用key的数字描述来代替hashing或者key的比较。基本的思路和在字母排序的字典中查找很相似:单词的第一个字母可以用来跳转到所有的以这个字母为起始的位置。在电脑中,这个过程可以一直持续到找到这个查询的对象。作为这个过程的结果,所有的操作都有O(k)的复杂度,k是key的长度。在有超大数据集的时代,n比k增长的更快,有一个时间复杂度独立于n的查询是一个很有吸引力的事情。
在本文里,我们陈述了adaptive radix tree(ART),这是一个快速的,空间效率高的内存索引结构,以及针对现在硬件做了专门的优化。当大部分radix tree都在基于一个全局的扇入扇出的参数做一个树的高度和空间使用效率的权衡时,ART适应了每个独立节点的描述,像图1那样。通过本地的适配了每个内部节点,他优化了全局的空间利用率同时能够有效的查询。为了效率和压缩数据,基于子节点的数量动态的选择了代表节点的一个很小的数字。两个额外的技巧,路径压缩和懒扩展,让ART能够更有效率的压缩内部节点来索引长key,以及减少树的高度。
radix tree一个非常有用的属性是key的顺序不是随机的;这些key是被按照字典序排列的。我们展示了这些典型的数据类型怎样被有效的排序,去支持所有的需要数据有序的操作(比如,范围查询,前缀搜索,top-k,最小,最大)。
本文做了下面的工作:
我们开发了adaptive radix tree (ART),一个快速和空间效率高的通用内存数据库系统的索引结构。
我们证明每个key的空间的放大是52字节,即使是任意长的key。我们的试验显示,空间放大实际上更低,大约为每个key 8.1字节
我们陈述了怎么把通用的数据类型存储到radix tree中,并且保持他们的顺序
我们试验评估了ART和别的主存索引结构,包括大部分的查找树
通过把ART集成到HyPer的主存数据库系统中,我们跑了TPC-C benchmark,我们证明了他在现实的数据库系统中特别牛逼的端到端性能。
本文的后面是这样组织的。下一章会讨论有关系的工作,第三章会展示adaptive radix tree和分析他的空间放大。第四章我们介绍了二进制比较Key的含义,以及怎么把通用的类型转为这种key。第五章描述了实验结果,包括几个benchmark和TPC-C benchmark。最后一章总结和讨论了未来的一些工作。
2. 相关工作
在基于磁盘的数据库系统中,B+tree无所不在。他会一下子从磁盘读很多数据以避免对磁盘的读取次数。红黑树和T-Tree也被用过内存数据库的索引。Rao和Ross显示,T-tree,像很多二叉查找树一样,受限于严重的cache不友好的行为,在现代硬件上经常比B+Tree慢很多。作为一个备选,他们们提出了一个cache友好的B+Tree变种,被称为CSB+Tree。更多的针对B+Tree的cache优化是Graefe和Larson做的。
现代CPU通过一个SIMD指令可以同时做多个比较操作。Schlegel et al.提出了K路查找,减少了比较次数从O(log2n)到O(logkn),k是一个SIMD vector能容纳的key的数量。同二叉树相比,这个技术可以减少cache miss的次数,因为K次比较是同时在每条从主存中load到cache line上执行的。Kim et al.提出的FAST扩展了这个研究,一个架构敏感的方式来存放二叉树的技术。SIMD,cache line,page blocking都被用来优化cache和内存带宽。另外,为了提高搜索算法的吞吐,他们提出插入多级流水线的查询。FAST树和K路查找树是没有指针的搜索数据结构,他们把所有的key存在一个数组里,然后用offset计算来遍历整棵树。尽管这种方式是查询快和节省空间的,但他也暗示了在线的插入是不可能的。Kim et al. 也提出了一个GPU的FAST实现,以及把它的性能和现代CPU做对比。结果显示,由于更高的内存带宽,GPU可以得到比CPU更多的吞吐。尽管如此,因为GPU的内存容量受限,同主存的通信成本很高,需要用几百个并行的查询来得到较高的吞吐,所以GPU作为索引硬件来使用不是特别实用。我们就把注意力集中在CPU的索引架构上来。
tries被用来索引字符串类型已经被研究的很广泛了。两个最早的变体用列表或者数组来做内部节点的形式。为了更有效的存储长string,Morrison提出了路径压缩的方法。Knuth很早就分析了这些trie变体。burst trie是一个更新一点的提议,树的高层节点用trie node,一但子元素数量少于某个数时就切换为链表。HAT-trie通过把链表切换为哈希表来提高性能。当大部分研究还在聚焦于索引字符串时,我们的目标是还能索引其他类型。所以相较于trie,我们更倾向于radix tree,因为它强调了排序算法的相似性和任意的数据都可以被索引。
Boehm et al. 首次提出了前缀树作为一个通用的检索结构。在SIGMOD Programming Contest 2009提出了一个fanout 16的radix tree。KISS-Tree是一个更有效的radix tree,它只有三层,却能存储32位的key。他用key的前16位和虚拟内存系统来节省存储空间。第二层用接下来的10位作为一个数组,最后一层用一个bit vector来压缩。Hewlett-Packard研究实验室发明的Judy数组数据类型可以动态改变内部节点。
Graefe讨论了可以二进制比较的key,作为一个简化和加速key比较的方法。我们用这些概念取得了radix tree里存储的key的顺序。
3. ADAPTIVE RADIX TREE
本章表述了Adaptive Radix Tree(ART)。我们基于一些在radix tree相较于比较树的优势开始。接下来我们说明了自适应的节点是必要的,因为传统的radix tree的空间占用非常显著。然后我们继续陈述了ART的查询和插入算法。最后我们分析了空间占用。
A 开场白
Radix tree有很多有趣的属性使他们和比较的搜索树完全不同:
Radix tree的高度和复杂度基于key的长度而不是元素的数目
Radix tree没有rebalance的操作,所有的插入顺序都会有同样的结果
key基于字典序来存储
叶子节点的路径代表了叶子的key。所以key可以用路径来重建出来
Radix tree包含了两种类型的节点:内部节点,通过key的一部分指向另外的节点;叶子节点,存储了相应key的数据。内部节点最有效的方式是一个2^s大小的数组。在树的遍历中,key的s位的一块作为数组中的索引,这样不用任何比较就可以找到下一个节点。参数s,我们成为span,对radix tree的性能来说非常重要,在key的长度确定时,树的高度也就确定了:一个存储了k bits key的radix tree的内部节点层数是 k/s层。以32bits为例,一个s=1的radix tree有32层,而一个s=8的tree只有4层。
在数据库系统中,基于比较的搜索树是非常普遍的索引结构,把radix tree的层数来和平衡搜索树的比较次数来对比就变得非常有意义。因为每次比较最好情况能排除1/2的数据,但radix tree可以排除更多的数据当s>1时。所以二叉树的高度比radix tree更高,n > 2^k/s。 图2说明了这种关系,假设key可以在O(1)的时间内比较完成。对于大key来说,key的比较一般需要O(k)的时间,因此搜索树的复杂度是O(klogn),而radix tree的复杂度是O(k)。观测结果证明,radix tree,特别是有一个很大的span的radix tree,会比传统的搜索树效率高很多。
B Adaptive Nodes
我们看到的是,从纯查询性能角度来看,一个大一些的span是好一点的。当指针数组被用来表示内部节点,一个大span的坏处也很明确:当大部分子节点是空的时候空间浪费非常严重。图三解释了保存100万个均匀分布的32位整数时,不同的span值,是对于空间和高度的权衡。span涨的时候,树的高度线性下降,但空间占用确成几何级数上涨。所以,实际上,只有几个s值可以提供一个相对合理的在时间和空间之间的权衡。举个例子, Generalized Prefix Tree 使用了4位的span,Linux内核中的radix tree用了6位。图三深度解释了我们的ART比radix tree有更小的高度和更小的空间,只是用了一些同质的节点数组。
得到空间和时间效率的关键思想是,在相同的相对来说比较大的span里用不同的节点大小,但是有不同的fanout。图四说明这个想法,而且展示了动态的节点并不影响树的结构,只是影响了节点的大小。通过减少空间放大,动态节点可以用更大的span,这样也提高了性能。
为了支持快速的动态更新,每次更新节点都去resize数组是代价很高的。所以我们用了几种节点的类型,没种都有一个不同的fanout。基于非空的孩子数,用一个合适的节点类型。当一个节点的容量由于插入而耗尽时,他会被一个更大的节点替代。相应的当一个节点被删除变得空洞时,他也会被一个小的节点类型替代。
C Structure of Inner Nodes
理论上说,内部节点通过key的一部分指引向子节点。内部我们用了四种不同容量的数据结构。给定一个关键的字节,每个数据结构都支持有效的查询删除插入一个子节点。另外,子节点允许被顺序扫描。我们用一个8位的span,对应key的一个字节,对应一个相对大的fanout值。这个选择还有一个优势就是简化了实现,因为字节可以直接被寻址避免了移位等操作。
图5展示了四种节点类型,然后根据最大容量来命名。相较于用一个kv对的列表,我们把列表分成了key的部分和指针的部分。这会使我们结构更紧密,查询效率更高。

Node4:他是最小的节点类型,可以保存最多4个子指针,用一个长度为4的数组保存key,用同样长度的数组保存指针。key和指针保存在对应的位置,而且key是有序的。
Node16: 这个节点类型用来保存5到16个孩子指针。像Node4一样,key和指针保存在不同的数组对应的位置,但是数组都有16个entry的空间。一个key可以通过二分查找来查询,在现代硬件上,还可以通过SIMD指令来做并行加速。
Node48: 当节点保存的entry数量增长的时候,key数组的查询也变得代价大了起来。所以超过16个指针的节点,不会直接保存key的内容。我们用一个256元素的数组来代替,可以直接用key的字节来索引。如果一个节点有17到48个孩子指针,这个数组把索引保存在第二个可以保存48个指针的数组。这种间接的方式可以在比较256个8字节的基础上节省空间,因为索引的部分只需要6位(我们用了1个字节来简化问题)。
Node256: 这是最大的节点类型,就是一个长度256的指针数组,用来保存49到256个entry。通过这种方式,下一个节点可以用一个字节就快速索引到。没有额外的间接信息。如果大部分entry不是空的时,这种表现也是非常有效率的,因为只需要保存指针。
另外,每个内部节点前面,有一个常数大小的header,保存了节点的类型,子节点的数量,和压缩的路径。
D Structure of Leaf Nodes
除了上一节提到的用内部节点保存路径外,radix tree必须保存和key对应的值。我们假设key是唯一的,因为非唯一的Key可以通过添加元组id来分别不同的key。
值用不同的方式来存储:
Single-value 叶子:只保存一个值的叶子类型
Multi-value叶子:值被保存在4个叶节点类型之一,和内部节点的四个类型一样,只不过保存了值而不是指针。
指针-值的 slots: 如果值和指针大小一样那么就不需要特殊的节点类型了。保存了一个指针的内部节点也可以保存一个指针或者值。值或者指针可以用指针的一个位来判断。
用Single-value叶子是最通用的方法,因为他允许同一个树里key和value有差异很大的长度。然而,因为树的高度一直在增长,每次查询都会导致额外的指针遍历。Multi-value叶子避免了这个问题,但是需要所有的Key都有同样的长度。Combined 指针/值 slots更有效率,允许存变长的key。所以如果合适的话,这种方法可以使用。用于数据库索引的二级存储就非常吸引人,通常是同样大小的标识符。
E Collapsing Inner Nodes
Radix tree有一个有用的属性就是每个内部节点都代表了一个key的前缀。所以key被明确的存储在树形的结构中,也可以从到叶子节点的路径重建出来。这可以节省空间,因为key不必被明确的存储起来。尽管如此,即使有前缀压缩和自适应节点,也有一些场景,特别是长key的时候,每个key的空间使用非常大。我们用两种额外的,广泛应用的技术来减少节点的数量来降低树的高度。这些技术对于长key来说非常有效,显著的提高了索引的性能。同样重要的是他们也减少了空间使用,在最坏的场景下确保了空间使用的边界。
第一个技术是lazy expansion,内部节点只有在需要辨别至少2个叶节点时才会被创建出来。图表展示了一个例子,lazy expansion节省了2个内部节点,通过把路径拼到叶子节点中"FOO"。 
如果插入了另外一个leaf前缀也是F的时候,这个path才会被展开。记住路径到叶子可能会被拼接,这种优化需要Key存在leaf节点或者是可以从数据库中读出来。
路径压缩是用到的第二个技术,移除了所有的内部节点,只有一个子节点。在图6中,内部节点保存了部分关键词的"A"被移除了。当然这种部分的key不能单纯的被忽略掉。有两种方式来解决:
悲观的:在每个内部节点,存储一个变长的部分key的vector。他包含了所有的移除了的单节点key。再查找这个vector的时候用来和搜索key比较,在下一个孩子节点以前。
乐观的:只有单节点的数量被保存了。查找只是跳过了这些字节。相应的当一个查找到一个叶节点的时候,他的key必须和叶节点作比较来确保没有错误发生。
这两种方法都保证了内部节点至少有2个孩子。乐观的方法在长string的时候特别有用,但是需要一个额外的检查,然而悲观的方法用了更多的空间,以及有了变长的节点大小,这也会导致内存碎片。我们用了一个混合的方法,跟悲观的方法一样,每个内部节点都保存了一个vector。但是所有的节点都是一样的大小。只有当大小溢出的时候,查询算法切换到乐观的策略。这样既不会浪费太多空间,也不会产生很多内存碎片。
F Algorithms
现在我们说明搜索和更新的算法:
搜索:搜索的伪代码像图7中的一样。用key连续的字节数组来遍历树,直到找到叶子节点或者空节点。第四行通过检查碰到的叶子完全匹配Key处理了lazy expansion。悲观的路径压缩在第七行和第八行处理,如果key和压缩路径不匹配便会终止搜索进程。下一个子节点通过findChild函数来查询,像图8显示的那样。基于节点类型,执行对应的搜索算法:因为一个Node4只有2-4个entry,我们用一个简单的loop就可以了。对于一个Node16,伪代码用了一个基于SSE指令集的SIMD的实现,允许在一个指令里并行比较16个key。首先,复制了搜索的key,然后把它和内部节点保存的16个key相比较。接下来,用一个mask,因为有些节点可能会少宇16个valid entry。比较的结果转化成了一个bit字段,然后应用了这个mask。最后,这个bit字段应用除0操作转化成了一个索引。或者说,在SIMD指令不能用的时候,可以用二分查找。搜索一个Node48,首先检查childIndex entry是不是有效的,然后返回对应的指针。Node256的搜索是指一个简单的数组寻址。 
插入:伪代码如图9所示。遍历树的操作通过递归调用实现,直到找到插入位置为止。通常,叶子可以只是插入到已经存在的内部节点中,如果需要就增大一些。或者,因为lazy expansion,可能会碰到一个存在的叶子,就会用一个新的内部节点替代包含已经存在的和新的叶子。另一个特殊的情况是如果新叶子的key和压缩路径不同:就需要在当前节点前面创建一个新的内部节点,压缩路径也要相应的调整。我们省略了一些helper函数,replace替换了一个Node用另外一个Node,addChild添加一个新孩子到内部节点里,checkPrefix对比了节点的压缩路径和key,然后返回了相同的字节数,grow替换了节点到一个更大的节点类型,loadKey从数据库把叶子的key取回来。
Bulk Loading: 当一个存在的关系需要创建一个索引时,接下来的递归算法可以用来加速索引重建:用每个key的第一个字节把所有的键值对分到256个分区中,创建一个对应的内部节点。在返回内部节点前,他的孩子都已经被递归的应用到了bulk loading过程中了,通过用key剩余的字节。
Delete: 删除的实现和插入相对称。叶子从内部节点中移除,如果有必要需要收缩一下。如果这个节点只有一个孩子,他就会被孩子替代,然后压缩路径跟着调整。 
G 空间占用
尽管TB级别的RAM服务器很容易就得到了,主存仍然是一个宝贵的资源。所以,索引结构应该足够的密集。对于radix tree来说,空间使用依赖于key的分布。密集的key是最好的情况,可以被有效的存储,尽管用了一个大的span和没有用上的adaptive nodes。当key特别稀疏时,很多内部节点的指针是空的,这会引起空间浪费。倾斜的Key使一些节点大部分都是空的,而另外一部分节点却非常密集。Adaptive nodes解决了这些问题,确保了任何Key的分布都会被压缩存储,每个节点根据自己的情况优化空间占用。
我们现在分析每个key的最坏的空间占用情况,考虑到adaptive nodes,lazy expansion和路径压缩。为了接下来的分析,我们假设指针都是8个字节的长度,每个节点有一个16字节的header保存了节点类型,非空孩子的数量,以及压缩路径。我们只考虑内部节点,忽略叶子节点,因为叶子不会有额外的空间使用,如果用上了绑定的键值对和tagged pointer的话。有了这些假设,每个节点类型的空间占用的分析如表所示 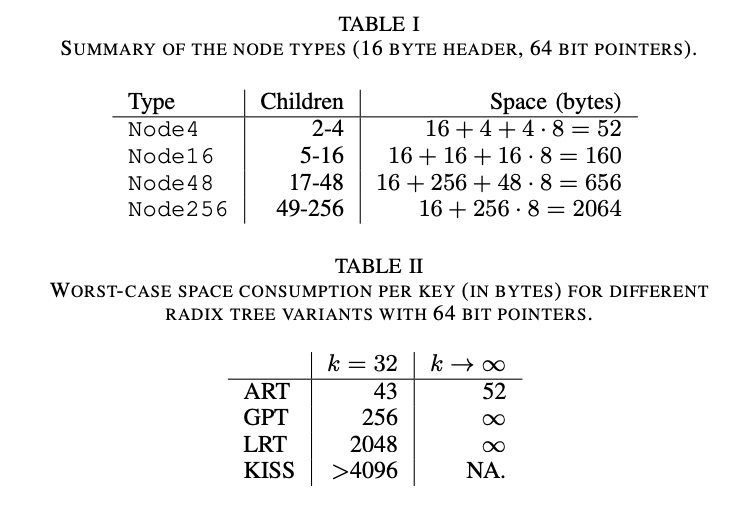
假设每个叶子节点提供x字节,内部节点占用孩子提供的空间。如果树的每一个节点都有一个确定的预算,那么树肯定每个key用的比x字节少。内部节点的预算就是他所有孩子节点的预算减去他的空间占用。正式地,把budget(n)作为节点n的预算,孩子节点的c(n)和空间占用s(n)被定义于下:

通过归纳所有的节点类型,我们发现如果x是52的话,所有的节点b(n) >= 52。对于叶子节点来说,和budget函数保持一致。为了证明内部节点也符合这个公式,我们算一个假设的最小值,和每个节点类型的子节点数。在减掉对应的空间占用后,我们算出了每个节点类型的最小预算。在四种情况下,都至少比52大,所以我们得出了这个结论。总结一下,x = 52的时候adaptive radix tree不能构建一个合理的节点。相应的,最坏的ART空间占用是52字节,即使是任意长的key。有6种节点类型的话,每个key的空间占用可以减少到34字节。像Section V-D里展示的一样,实际上空间占用要比最快情况好很多,即使是相对长的key。最好情况是8.1字节,经常可以得到这个数值,因为key一般密度都是比较大的。
让我们同Table II总结的radix tree做个对比,由于Generalized Prefix Tree和Linux kernel radix tree没有做路径压缩,内部节点的数量和key的长度成固定比例,所以最坏的平均空间占用是不固定的。而且,尽管是短key,由于没有自适应节点,这些数据类型在最坏情况下空间占用仍比ART要高很多。KISS-Tree最坏空间占用是每个key 4KB,比如用无符号整形的key时,i · 2 16 |i ∈ {0, 1, . . . , 2 16 − 1}}。
4 CONSTRUCTING BINARY-COMPARABLE KEYS
选择索引结构的重要的一点是数据是否被顺序存放。有序的索引结构是支持范围查询,最大,最小,top-N的必要支持。一般只有基于比较的树才会把数据顺序存放,这也导致了这种数据结构在数据库中的流行。尽管有顺序的哈希表,这种方式在现实中并不太常用。原因是不同分布的值很难在保持顺序的同时均匀的分布到哈希表里。radix tree中的key保存成了二进制的字典序。对于一些数据类型来说,比如ASCII编码的字符串,他可以产生预期的顺序。对于大部分数据类型来说不是这种情况。比如负的整数补码比正数要大。然而通过转换key是可以得到想要的结果的。我们把这种转换得到key称为可比较的key。只有当这种可二进制比较的key作为radix tree的key的时候,数据可以被有序存储,依赖有序存储的操作也都可以支持。需要注意的是上一节的算法是没有变化的,只不过所有的key在保存和查找前要先转换为可二进制比较的key。
Binary-comparable key还有其他使用场景。就像可以把基于比较的tree替换为radix tree一样,基于比较的排序算法比如快速排序和归并排序都可以替换为基数排序,可以有很高的渐进效果。
A. Definition
转换方程t : D → {0, 1, . . . , 255} k,把D内的值转换为k长度的binary-comparable key,如果他满足下面的等式。

操作符<,>,=表示输入类型的操作符可以用memcmp-k两种元素的vector来实现。如果返回0表示左右的数据都是相等的,负值代表第一个不等的元素是第一个vector小于第二个,正值相反。
对于有限的数据集,总能找到转换的方法:size为N的数据集被映射到log2N 位的string上。
B. Transformations
我们现在讨论一下怎么把通用的数据类型转换到binary-comparable key。
Unsigned Integers 无符号整数的二进制形式已经
Signed Integers 有符号数必须要转换,因为负数是降序而且比正数大
IEEE 754 Floating Point Numbers
字符串
NULL
复合key 包含了多重属性的key可以很容易的做每个属性的转换,然后联合起来
5 EVALUATION
本节我们评估了ART和其他索引数据类型的性能对比,包括基于比较的tree,哈希表和radix tree。评估分为两个部分,首先,我们做了所有评估数据结构的的benchmark。其次,我们把这些数据结构集成到了内存数据库HyPer中。这可以使我们执行一个更加真实的工作负载,标准的OLTP benchmark TPC-C。我们用了一个高端的桌面系统Intel Core i7 3930K CPU,有6个核12线程,主频3.2GHz,3.8GHz超频。系统有12MB的共享底层cache,和32 GB的主存。操作系统是64位Linux 3.2,编译器GCC 4.6。
比较对手,我们用了:
内存优化的B+tree (Cache-Sensitive B +-tree [CSB])
两个针对x86 CPU优化的只读结构 (k-ary search tree [kary], Fast Architecture Sensitive Tree [FAST])
radix tree (GPT)
两个教科书上的数据结构,红黑树和哈希表
公平起见,我们尽量用作者提供的源码。CSB+-Tree,k-ary search, GPT都是这样的。其余的数据结构我们自己实现了。
我们确保我们自己实现的FAST和公布的性能是一样的。为了统一不同的硬件,我们用了k-ary search发表在同一篇paper上的结果。我们FAST的实现用了2MB的内存页,把所有的cacheline对齐到64字节的cache line,像Yamamuro建议的那样。然而,FAST和k-ary search返回了key的位置而不是元组ID,为了衡量一个有效的数据库查询结果,接下来的结果包含了一次额外的数组查询。
在micro benchmark里我们用了32位的int作为key,因为一些实现只支持32位的整数key。对于很短的key来说,路径压缩经常增加了空间使用而不是减少它。所以在benchmark测试里我们移出了这个功能。在第二阶段的评估里,路径压缩都是开启的。和基于比较的tree以及哈希表相比,radix tree在key的分布不一样的时候性能差异很大。所以我们测试了从0到n的密集key,n是key的取值范围,以及每位不是0就是1的稀疏的key。我们随机的重新排列了这些密集的key。
A. Search Performance
在我们第一个实验里,我们测试了随机查找的性能,下图显示ART和哈希表有最好的查找性能。ART比GPT要快两倍。红黑树是最慢的比较树,其次是CSB+Tree,k-ary search和FAST。尽管FAST不支持更新和针对现代硬件做了优化,但他仍比ART和哈希表要慢。数据结构的相对性能和index的大小非常相关。数据显示65K的索引要比256M的索引快十倍,这说明影响性能的是cache的效率而不是数据结构的属性。

为了更好的理解这些结果,看下表格三,它显示了ART,FAST和哈希表每次随机查找的性能指标。有16M key的时候,只有一部分的内存结构被cache了,查找是内存密集的。cache miss的数量,FAST和哈希表以及稀疏的ART基本一样。在密集key的场景,ART可以减少一半的cache miss,因为他可以把节点压缩成cache友好的形式。在树比较小的时候,查询性能主要受指令数和分支预测失败影响。但ART在密集key的场景基本没有分支预测失败,稀疏的key大约每次lookup有0.85次分支预测失败。密集的key需要更少的指令,因为在Node256里找下一个child不需要额外的计算,其他的节点类型可能会付出更大的代价。和通常的比较树相比,FAST避免了分支预测失败,但是需要更多的指令数来达到这个效果。哈希表则在冲突时有少量的分支预测失败。

到目前位置,查找都是在一个线程里,依次查询的。下一个试验的目标就是用多线程找到最佳吞吐。除去多线程,另一个有效提升吞吐的方法是用软件的流水线。这种技术充分利用了现代CPU的superscalar特性,但显著增加了延迟。FAST受益于软件流水线最大2.5倍,这样它比较大的比较延时和地址计算可以被掩盖起来。由于ART的计算量较小,但他在软件流水线也有显著受益,大约有1.6倍到1.7倍。哈西链表可以想象为只有两级(哈西数组和kv对的列表),所以加速效果最差,大约只有1.2倍。图表11显示了尽管用了11个线程,每个线程8个并发的查询,ART的稀疏key也仅仅比FAST慢一点,但密集key确明显要快很多。

B Caching Effects
接下来我们调查一下cache的影响。对现代CPU来说,cache变得极端重要,因为DRAM的延迟是CPU cycle的几百倍。树的结构受益于cache影响跟大,因为频繁访问的节点路径上顶部节点一般都被cache了。为了定量的分析cache的影响,我们对比了两种数据结构(密集key的ART和FAST)和哈希表。
至今为止我们做的这些随机查询对cache来说是最坏的,因为这些访问没有聚集性。实际上,查询区域的热点是非常普遍的,最近的查询区域会比老的查询区域更热。我们模拟了一个Zipf分布的场景来替代随机key。图表12显示了偏斜的数据区域对性能的影响程度。当数据倾斜时,所有的性能都变好了,因为cache miss变少了。随着倾斜程度增加,ART和哈希表的性能缓慢接近在小数据量的cache无关的结果。而对于FAST来说加速有限,因为他需要更多的比较和offset计算,这些都不会被cache影响。
现在我们把焦点放在cache大小的影响上,在前面的实验里,我们只是做了单个tree的查询。所以,所有的内存都被利用起来了,也没有内存访问的竞争。通常cache会有多种索引和其他的数据。为了模拟访问竞争和小的cache size,我们round-robin的方式依次访问多种数据结构。每种数据结构保存了16M个密集的Key,占用了超过128M空间。图表13显示,哈希表收到影响最小,因为他也不怎么有效的用cache。随着cache size越来越大,经常放的路径被cache的也越来越多。当只有1/64的cache时(192KB),ART的性能只有全部cache(12MB)的1/3。
C Updates
除去查询的效率,一个索引结构也必须支持有效的更新。图表14显示了当插入14M个随机key到空的结构时候的吞吐。尽管ART需要动态的替换他的内部节点,他也比其他数据结构更有效率一点。同全部用Node256相比,自适应的节点对插入性能的应该大约是20%。而且自适应节点大量减少了内存使用,所以这是一个非常值得的tradeofff。在增量插入方面,bulk插入可以提高2.5倍稀疏key的性能,但只能提高17%密集key的性能。当排序key,作为主key的替代时,由于cache影响能提高查询性能。对于ART来说,50M个有序的密集的key可以在1s内插入。只有哈希表没有在有序方面受益,因为他随机化了访问pattern。

FAST和k-ary搜索树是静态的数据结构,只能通过重建来更新他们,这也是为什么前面的试验没有测试他们。一个在应用中用只读数据结构的机制是一种delta的方式:一个额外的数据结构,支持在线插入,定期的和只读结构合并。为了评估这种方式的可行性,我们用红黑树作为delta数据结构,加上FAST作为主索引,并把它和ART以及哈希表对比。我们试验了多种delta和FAST间的合并频率。我们的工作负载是在一个16M个元素的树里随机的插入,删除,查询。图15显示了不同占比下的结果。当查询占比减少时,FAST+delta的性能就会下降,因为额外合并的效率比较低。

D. End-to-End Evaluation
在端到端的应用实验中,我们用了主存数据库系统HyPer。他的一个特定就是可以同时支持OLAP和OLTP的工作负载。事务用一个脚本语言来实现,然后被编译成了类似LLVM的指令。而且,HyPer没有额外的buffer管理,锁和同步机制。所以他的性能严重依赖于索引结构的有效性。对于每个索引,HyPer允许指定不同的索引结构。哈希表和红黑树都是原生支持的。我们把ART集成了进去,包括路径压缩,懒扩展等优化。而且我们还做了key的转换,这样可以支持范围查询,前缀搜索,最小,最大等。
接下来的试验用TPC-C测试,一个标准的OLTP benchmark,他模拟了一个商业公司去管理,销售,分发商品。他有很多种不同的查询,包括点查询,范围查询和前缀搜索,和插入删除。虽然他被认为是一个写很重的benchmark,但他54%的sql语句都是查询。我们的测试忽略了client的时间,用一个5个仓库的数据集。我们跑benchmark直到所有的RAM都被耗尽。索引我们用了ART,红黑树,红黑树和哈希表的结合。不能所有的索引都用哈希表,因为TPC-C有时候会在某些索引上做前缀的范围搜索。
图表16说明,索引的选择对于HyPer的性能来说非常重要。ART的性能基本是哈希表+红黑树的2倍,是红黑树的4倍。哈希表有效的提高了红黑树的性能,但在rehash的时候对性能有明显的影响。

在benchmark的后期,我们把注意力转移到空间使用上来。为了节省空间,HyPer的红黑树和哈希表都不会直接保存key,而是一个统一标识符。用了标识符后,key按需从数据库中加载。尽管在最坏情况下,ART每个元素会用更多的内存,在这个实验中,ART只用了红黑树和哈希表一半的空间。更细节的空间分析可以从表四中每个key的平均空间占用来获得。

Index3每个key用了更多的空间,因为它保存了相对长的string。尽管如此他的空间占用也比最坏情况的52个字节要好。Index 1, 2, 4, 5平均每个key只用了8.1个字节,因为他们保存了密集的整数。Index 6, 7在这两种极端情况之间。
我们最终的实验结果在图表17,衡量了路径压缩和懒扩展在树平均高度方面的影响。默认,radix tree的高度就是key的字节数。举个例子,Index3如果没有任何优化的话,高度是40。路径压缩和懒扩展把树的高度降到了8.1。懒扩展在长string的情况下非常有效。路径压缩在长string的情况下也很有用,以及有同样前缀的密集的int,比如index 2, 4, 5, 7。两种优化在空间占用方面的影响和树的高度差不多,所以我们没有额外展示。总结一下,除了短int,路径压缩和懒扩展是radix tree能得到高性能和低内存占用的关键因素。
6 CONCLUSIONS AND FUTURE WORK
本文我们发表了adaptive radix tree,一个快速而且内存占用少的数据库索引结构。一个高的fanout,路径压缩和懒扩展,结合起来实现了高性能。radix tree普遍的问题,在最坏情况下的内存占用,被动态的压缩内部节点来解决了。我们对比了ART和其他的内存索引结构。我们的试验结果显示,ART比CSB+Tree, GPT, 以及其他的radix tree要快。即使是针对现代CPU专门优化过的只读数据结构FAST也比ART要慢,而且还没考虑到它不能更新。在所有评估的数据结构里面,只有哈希表的性能是差不多的。但是哈希表是无序的,不能作为统一的数据结构来用。通过把ART放到HyPer中跑TPC-C benchmark,我们证明ART在事务场景的索引结构方面是一个非常优秀的替代者。
在未来,我们在并发更新方面会投入更大精力。特别的,我们计划利用CAS开发一个无锁的同步机制。另一个想法就是用相同大小的节点实现一个空间有效的radix tree。和依据key的稀疏程度动态的改变fanout相比,key占用的bits可以动态的改变,这样fanout就变成常量。这样的tree可以被当做磁盘上的数据结构。
最后更新于